ley de snell
Ley de Snell de la refracción
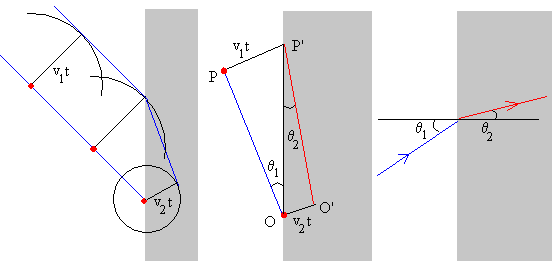
Consideremos un frente de ondas que se acerca a la superficie de separación de dos medios de distintas propiedades. Si en el primer medio la velocidad de propagación de las ondas es v1 y en el segundo medio es v2 vamos a determinar, aplicando el principio de Huygens, la forma del frente de onda un tiempo posterior t.
A la izquierda, se ha dibujado el frente de ondas que se refracta en la superficie de separación de dos medio, cuando el frente de ondas incidente entra en contacto con el segundo medio. Las fuentes de ondas secundarias situadas en el frente de ondas incidente, producen ondas que se propagan en todas las direcciones con velocidad v1 en el primer medio y con velocidad v2 en el segundo medio. La envolvente de las circunferencias trazadas nos da la forma del frente de ondas después de tiempo t, una línea quebrada formada por la parte del frente de ondas que se propaga en el primer medio y el frente de ondas refractado que se propaga en el segundo.
El frente de ondas incidente forma un ángulo θ1 con la superficie de separación, y frente de ondas refractado forma un ángulo θ2 con dicha superficie.
En la parte central de la figura, establecemos la relación entre estos dos ángulos.
-
En el triángulo rectángulo OPP’ tenemos que
v1·t=|OP’|·senθ1
-
En el triángulo rectángulo OO’P’ tenemos que
v2·t=|OP’|·senθ2
La relación entre los ángulos θ1 y θ2 es
![]()
Reflexión total
-
Si v1>v2 el ángulo θ1 > θ2 el rayo refractado se acerca a la normal
-
Si v1<v2 el ángulo θ1 < θ2 el rayo refractado se aleja de la normal
En este segundo caso, para un ángulo límite θc el ángulo de refracción es θ2 =π/2
![]()
El ángulo límite es aquél ángulo incidente para el cual el rayo refractado emerge tangente a la superficie de separación entre los dos medios.
Si el ángulo de incidencia es mayor que el ángulo límite, el seno del ángulo de refracción resulta mayor que la unidad. Esto indica, que las ondas que inciden con un ángulo mayor que el límite no pasan al segundo medio, sino que son reflejados totalmente en la superficie de separación.
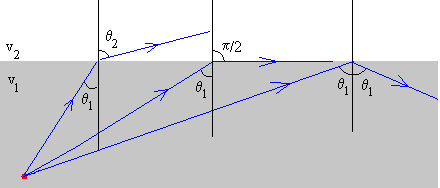
En la figura, observamos que a medida que se incrementa el ángulo de incidencia θ1 el ángulo de refracción aumenta hasta que se hace igual a π/2. Si se vuelve a incrementar el ángulo de incidencia, la onda incidente se refleja en el primer medio.
Índice de refracción
Se denomina índice de refracción, al cociente entre la velocidad de la luz c en el vacío y la velocidad v de la luz en un medio material transparente.
n=c/v
La ley de Snell de la refracción se expresa en términos del índice de refracción
n1·senθ1= n2·senθ2
