Tubos sonoros
|
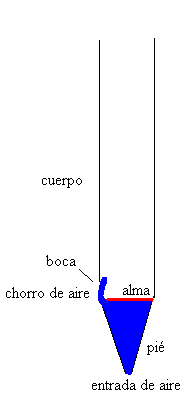
Las versiones modernas de estos instrumentos de viento son las flautas, las trompetas y los clarinetes, todos ellos desarrollados de forma que el intérprete produzca muchas notas dentro de una amplia gama de frecuencias acústicas. El órgano es un instrumento formado por muchos tubos en los que cada tubo da una sola nota. El órgano de la sala de conciertos de La Sydney Opera House terminado en 1979 tiene 10500 tubos controlados por la acción mecánica de 5 teclados y un pedalero. El tubo de órgano es excitado por el aire que entra por el extremo inferior. El aire se transforma en un chorro en la hendidura entre el alma (una placa transversal al tubo) y el labio inferior. El chorro de aire interacciona con la columna de aire contenida en el tubo. Las ondas que se propagan a lo largo de la corriente turbulenta mantienen una oscilación uniforme en la columna de aire haciendo que el tubo suene.
|
Los tubos de caña o de otras plantas de tronco hueco, constituyeron los primeros instrumentos musicales. Emitían sonido soplando por un extremo. El aire contenido en el tubo entraba en vibración emitiendo un sonido.Ya hemos visto en este capítulo como son las ondas estacionarias en una cuerda. Ahora veremos las ondas estacionarias que se producen en los tubos abiertos o cerrados por un extremo.
Tubos abiertos
 |
 |
 |
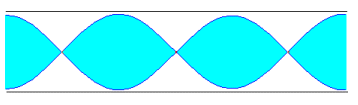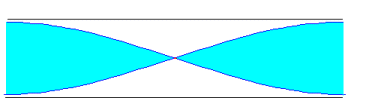
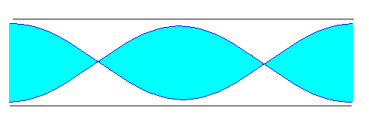
Si un tubo es abierto, el aire vibra con su máxima amplitud en los extremos. En la figura, se representan los tres primeros modos de vibración
Como la distancia entre dos nodos o entre dos vientres es media longitud de onda. Si la longitud del tubo es L, tenemos que
L=l /2, L=l , L=3l /2, ... en general L=nl /2, n=1, 2, 3... es un número entero
Considerando que l =vs/f (velocidad del sonido dividido la frecuencia)
Las frecuencias de los distintos modos de vibración responden a la fórmula
Tubos cerrados
 |
 |
 |
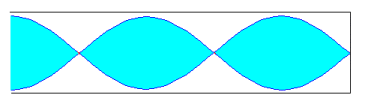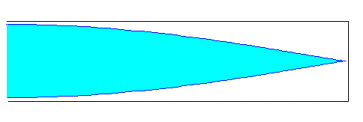
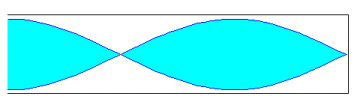
Si el tubo es cerrado se origina un vientre en el extremo por donde penetra el aire y un nodo en el extremo cerrado. Como la distancia entre un vientre y un nodo consecutivo es l /4. La longitud L del tubo es en las figuras representadas es L=l /4, L=3l /4, L=5l /4...
En general L=(2n+1) l /4; con n=0, 1, 2, 3, ...
Las frecuencias de los distintos modos de vibración responden a la fórmula