refraccion y lentes
La refracción de la luz

Se denomina refracción luminosa al cambio que experimenta la dirección de propagación de la luz cuando atraviesa oblicuamente la superficie de separación de dos medios transparentes de distinta naturaleza. Las lentes, las máquinas fotográficas, el ojo humano y, en general, la mayor parte de los instrumentos ópticos basan su funcionamiento en este fenómeno óptico.
El fenómeno de la refracción va, en general, acompañado de una reflexión, más o menos débil, producida en la superficie que limita los dos medios transparentes. El haz, al llegar a esa superficie límite, en parte se refleja y en parte se refracta, lo cual implica que los haces reflejado y refractado tendrán menos intensidad luminosa que el rayo incidente. Dicho reparto de intensidad se produce en una proporción que depende de las características de los medios en contacto y del ángulo de incidencia respecto de la superficie límite. A pesar de esta circunstancia, es posible fijar la atención únicamente en el fenómeno de la refracción para analizar sus características.
Las leyes de la refracción
Al igual que las leyes de la reflexión, las de la refracción poseen un fundamento experimental. Junto con los conceptos de rayo incidente, normal y ángulo de incidencia, es necesario considerar ahora el rayo refractado y el ángulo de refracción o ángulo que forma la normal y el rayo refractado.
Sean 1 y 2 dos medios transparentes en contacto que son atravesados por un rayo luminoso en el sentido de 1 a 2 y e1 y e2 los ángulos de incidencia y refracción respectivamente. Las leyes que rigen el fenómeno de la refracción pueden, entonces, expresarse en la forma:
1.ª Ley. El rayo incidente, la normal y el rayo refractado se encuentran en el mismo plano.
2.ª Ley. (ley de Snell) Los senos de los ángulos de incidencia e1 y de refracción e2 son directamente proporcionales a las velocidades de propagación v1 y v2 de la luz en los respectivos medios.
![]()
Recordando que índice de refracción y velocidad son inversamente proporcionales la segunda ley de la refracción se puede escribir en función de los índices de refracción en la forma:
![]()
o en otros términos:
n1 · sen e1 = n2 · sen e2 = cte
Esto indica que el producto del seno del ángulo e por el índice de refracción del medio correspondiente es una cantidad constante y, por tanto, los valores de n y sen e para un mismo medio son inversamente proporcionales.
Debido a que la función trigonométrica seno es creciente para ángulos menores de 90º, de la última ecuación se deduce que si el índice de refracción ni del primer medio es mayor que el del segundo n2, el ángulo de refracción e2 es mayor que el de incidencia e1 y, por tanto, el rayo refractado se aleja de la normal.
Por el contrario, si el índice de refracción n1 del primer medio es menor que el del segundo n2, el ángulo de refracción e2 es menor que el de incidencia el y el rayo refractado se acerca a la normal.
Estas reglas prácticas que se deducen de la ecuación son de mucha utilidad en la representación de la marcha de los rayos, operación imprescindible en el estudio de cualquier fenómeno óptico desde la perspectiva de la óptica geométrica.
La refringencia de un medio transparente viene medida por su índice de refracción. Los medios más refringentes son aquellos en los que la luz se propaga a menor velocidad; se dice también que tienen una mayor densidad óptica. Por regla general, la refringencia de un medio va ligada a su densidad de materia, pues la luz encontrará más dificultades para propagarse cuanta mayor cantidad de materia haya de atravesar para una misma distancia. Así pues, a mayor densidad, menor velocidad y mayor índice de refracción o grado de refringencia.
Lentes convergente y divergentes
Un lente convergente o biconvexo, es un lente donde los rayos de luz convergen, hacia el foco del lente, y donde su distancia focal ( f), es mayor que cero.
La imagen en un lente convergente puede ser real o virtual, dependiendo de la posicion del objeto, si el objeto esta entre el foco y el lente, entonces, la imagen sera virtual y mas grande que el objeto.

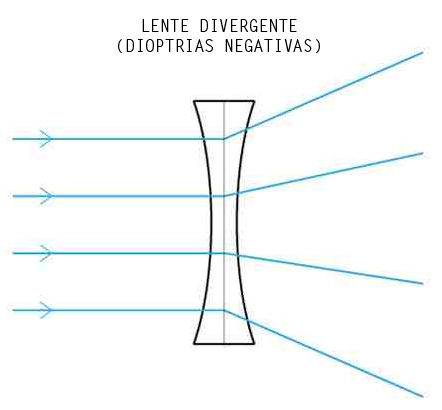
En un lente divergente, la distancia focal es menor que cero, donde la imagen siempre sera virtual, es por eso que es un lente divergente, los rayos de luz, no convergen, sino luego de chocar con la superficie del lente, se separan, divergen, esto hace una imagen por lo general mas pequeña y virtual.
Las reglas generales paratrazar diagramas de rayos con lentes se parecen a la de los espejos esféricos,pero se necesitan algunas modificaciones, Porque:
“laluz atraviesa la lente, y no se refleja en ella”.

Los tres rayos de un punto de un objeto se trazan como sigue:
Lentes Convergentes
1. Un rayo paralelo
Pasa por el foco del lado de la imagen de una lente convergente

2. Un rayo central o rayo principal es el que pasa por el centro dellente y no se desvía.

3. Un rayo focal
Pasa por el foco del lado del objeto en una lente convergente, y después
de atravesarla, es paralelo al eje óptico de ella


Acción de una sección delente convergente sobre un haz de rayos paralelos.

Laslentes convergentes pueden formar imágenes virtuales mayores que el objeto
(Lupa).

Lentes Divergentes
1. Rayo Paralelo parece emanar del foco, del lado del objeto, en el ladodel objeto de una lente divergente
2. Un rayo central o rayo principal es el que pasa por el centro dellente y no se desvía.
3. Un rayo focal es paralelo al eje óptico de una lente divergente y despuésde atravesarla parece provenir del foco del lado del objeto en una lentedivergente.

Acción de una sección delente divergente sobre un haz de rayos paralelos.

Laslentes divergentes siempre forman imágenes virtuales menores que el objeto.

La ecuación del constructor de lentes
Procederemos a deducir la ecuación del constructor de lentes, que es una relación entre la longitud focal f, el índice de refracción n de la lente y los radios de curvatura R1 y R2 de las superficies de la lente. Utilizamos el principio de que una imagen formada por una superficie reflectora o refractora puede servir como objeto para una segunda superficie reflectora o refractora.
Empezamos con el caso un poco más general de dos superficies esféricas que separan tres materiales con índices de refracción na,nb y nc, como se muestra en la figura 42. Las distancias objeto e imagen para la primera superficie son s1 y s1' y las correspondientes a la segunda superficie son s2 y s2'. Suponemos que la lente es delgada, de modo que la distancia t entre las dos superficies es pequeña en comparación con las distancias objeto e imagen y, por tanto, se puede despreciar. Entonces, s2 y s1' tienen la misma magnitud y el signo opuesto. Por ejemplo, si la primera imagen se encuentra en el lado por donde se alejan los rayos de la primera superficie, s1' es positiva. Pero cuando se le considera como un objeto para la segunda superficie, la primera imagen no se encuentra en el lado de esa superficie por donde inciden los rayos, de modo que podemos decir que s2 = -s1'.

figura 42
Necesitamos utilizar la ecuación para una sola superficie, ecuación 4 del apartado Imágenes formadas por refracción, dos veces, una para cada superficie. Las dos ecuaciones resultantes son:
![]()
![]()
Por lo general, el primero y el tercer materiales son aire o el vacío, de modo que hacemos na = nc = 1. El segundo índice de refracción nb es el de la lente, que denotaremos simplemente con n. Al sustituir estos valores y la relación s2 = -s1' obtenemos:
![]()
![]()
Para obtener una relación entre la posición inicial del objeto s1 y la posición final de la imagen s2', sumamos estas dos ecuaciones. Con ello eliminamos los términos n/s1' y obtenemos:
![]()
Finalmente, considerando la lente como una sola unidad, llamamos a la distancia objeto s, en vez de s1, y s' a la distancia imagen final en lugar de s2'. Haciendo estas sustituciones tenemos:
![]()
Ecuación 1.
Ahora comparamos esta expresión con la otra ecuación para lentes delgadas, la ecuación 3 del apartado Propiedades de una lente. Vemos que las distancias objeto e imagen s y s' aparecen exactamente de la misma forma en ambas ecuaciones, y que la longitud focal f está dada por:
![]()
(ecuación del constructor de lentes para una lente delgada).
