numeracion binaria
El sistema numérico binario utiliza como base el 2, que corresponde al número de dígitos que se utilizan para representar cantidades. Estos dígitos son 0 y 1 que se conocen como “bits” abreviadamente. Por tal razón un número binario es una sucesión de bits, posiblemente con un punto binario intercalado.
Al igual que el sistema decimal, el sistema binario es posicional, por lo cual cada dígito tiene un valor relativo a la posición que ocupa en el número. El valor de posición en este sistema se consigue multiplicando el dígito por una potencia de 2. A continuación se explica como sacar la potencia a cualquier numero y se muestra una tabla con los valores posiciónales de los dígitos en el sistema numérico binario y Decimal.
Binario Solamente tiene 2 Valores Llamados bits.
bit (b): 1 = V = Presencia de Voltaje = 5 Voltios
bit (b): 0 = F = Ausencia de Voltaje = 0 Voltios
Ahora 8 bits forman 1 Byte
Byte (B) = 00000000 8 ceros
Byte (B) = 11111111 8 unos
Byte (B) = 01011001 8 ceros y unos
Pregunta:

Para Pasar a un Numero Decimal........
Entonces:
El Lenguaje Binario que es el lenguaje de cualquier equipo Digital tiene 2 valores el 0 y el 1, por tanto su Base es 2.
y Lenguaje Decimal que es el lenguaje Humano tiene 10 valores el 0,1,2,3,4,5,6,7,8,9,, por tanto su Base es 10.
Formula para Encontrar Potencias
Be = P
Donde B es Igual a BASE
Donde e es Igual a EXPONENTE
Donde P es Igual a la POTENCIA
Nota:
Todo Numero Base Elevado al exponenete 0 es igual a 1: B0 = 1
20 = 1
30 = 1
40 = 1
.
.
.
100 = 1
El Resto de Numeros Base con exponenetes mayores de 1, se encuentra su Potencia multiplicando el numero de veces el exponente de su Base.
Ejemplo
|
Lenguaje Binario |
Lenguaje Decimal
|
|
20 = 1 21 = 2*1 = 2 22 = 2*2 =4 23 = 2*2*2 = 8 24 = 2*2*2*2 = 16 25 = 2*2*2*2*2 = 32 26 = 2*2*2*2*2*2 = 64 27 = 2*2*2*2*2*2*2 = 128
Truco 1 para sacar 28 puedo multiplcar la potencia de 27 por 2 y haci sucesivamente. Ejm
28 = 128 * 2 = 256
29 = 256 * 2 = 512
210 = 512 * 2 = 1024
|
100 = 1 101 = 10*1 = 10 102 = 10*10 = 100 103 = 10*10*10 = 1000 104 = 10*10*10*10 = 10000 105 = 10*10*10*10*10 = 100000 106 = 10*10*10*10*10*10 = 1000000 107 = 10*10*10*10*10*10*10 = 10000000
Truco 2 El Truco Para sacar la potencia de cualquier numero decimal es colocando el 1 el 0 el numero de veces que da el exponete. Ejm 103 = El 1 y 3 veces el 0 = 1000 108 = El 1 y 8 veces el 0 = 100000000
|
La Tabla 1 muestra los valores de los dígitos de un número binario.
Tabla 1
|
Valores Posiciónales en el Sistema Binario |
||||||||||
|
Potencia de dos |
|
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
|
|
Valor |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
|
|
“Al igual que en el sistema decimal, en el sistema binario las potencias aumentan de derecha a izquierda”

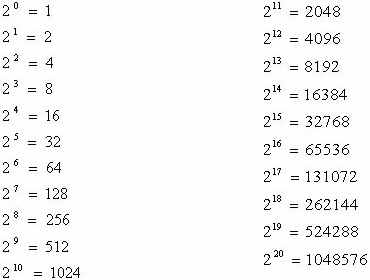
La Forma Facil de Encontara cual es el valor de un Numero Decimal se ilustra en la siguiente Tabla.
|
27
|
26
|
25
|
24
|
23
|
22
|
21
|
20
|
Potencia |
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Decimal |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
20 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
128 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
129 |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
130 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
240 |
|
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
23 |
Truco 3
El Truco esta en Sumar solamente los bits con valor 1
|
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
Potencia |
|
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Decimal |
|
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
148 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
132 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
133 |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
42 |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
5 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
198 |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
15 |
Otra de Forma de Sacar un Numero Decimal es con la Notacion Expandida
La notación expandida de número es la sumatoria de sus valores posiciónales. Por ejemplo, considere el número binario 10101. La notación expandida de este número está dada por:
10101 = 1×24 + 0×23 + 1×22 + 0×21 + 1×20 = 16 + 0 + 4 + 0 + 1
Para encontrar el equivalente decimal de un número binario sólo tenemos que resolver la notación expandida.
El equivalente decimal del número binario anterior es 21. Para distinguir un número binario de uno decimal, utilizaremos un sub-índince de 2 al final del número binario.
En la Tabla 2 se muestra la representación binaria de 8 bits, o sea de un Byte de los primeros 11 números enteros no negativos.
Tabla 2
|
Números Decimales y Binarios |
|
|
Enteros No negativos |
Equivalente Binario |
|
0 |
00000000 |
|
1 |
00000001 |
|
2 |
00000010 |
|
3 |
00000011 |
|
4 |
00000100 |
|
5 |
00000101 |
|
6 |
00000110 |
|
7 |
00000111 |
|
8 |
00001000 |
|
9 |
00001001 |
|
10 |
00001010 |
